In horary astrology, the 5-degree rule is of everyday use. The essence of the law is simple. If the planet is close to the next house's cusp (closer than 5 degrees and in the same sign as the cusp), then the planet is already in the next house.
If we interpret the rule literally after William Lilly, we will certainly fall into a trap. Imagine you are in the North, and your horary chart looks like this:
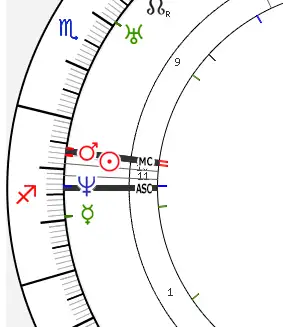
The Sun is obviously at the top of the 10th house. But according to the formal rule of 5 degrees, it is already in the 11th and even in the 12th house. So what house is the Sun? Unclear.
Intuitively, for narrow houses, 5 degrees should turn into something insignificant (half a degree-degree).
- But does this mean that for extensive houses, 5 degrees should turn into 7-8?
- Where is the proportion between the 5-degree gap and the width of the house, which we must adhere to?
To answer this question, we must recall the origins of this rule.
[toc]
Where did the 5-degree rule originate?
For the first time, this rule is mentioned by Ptolemy in his tetrabiblos, speaking about the duration of life. He says of 5 mundane degrees - if a planet is closer than five spatial degrees to the cusp of the angular house, then it is considered to belong to the angular house.
An important conclusion. Ptolemy spoke of 5 mundane degrees, not five zodiacal ones. It completely changes the picture of the rule.
What are the five mundane degrees in the system of houses of Regiomontanus?
Most astrologers, following Lilly, use the Regiomontanus house system to cust horary charts. This approach has proven itself well, so let's not break the tradition and stick to this house system.
What do house cusps look like in the Regiomontanus system?
To understand spatial degrees, one must start with the basics of celestial geometry. If you haven't read the article on primary directions yet, I recommend doing so.
Just in case, I will repeat here the basics of celestial geometry.
- The line of intersection of the plane under the feet of the observer with an imaginary celestial sphere is a circle called the horizon.
- The line drawn from the North through the zenith to the South is called the primary meridian.
- The celestial sphere rotation axis deviates from the horizon by an angle called the geographic latitude of the observer. For an observer at zero latitudes, this axis directs to the North.
- The plane perpendicular to the axis of rotation, dividing the celestial sphere in half, is called the celestial equator. The celestial equator crosses the horizon at the point of East and West.
- The plane that cuts the celestial sphere in half, and deviates from the equator by 23 degrees, is called the ecliptic, and its circumference is called the zodiac circle.
- The points of intersection of the ecliptic and the equator are 0º Aries/Libra on the zodiacal circle and 0º/180º right ascension in the plane of the celestial equator.
- The directions of the celestial sphere's daily rotation and the yearly movement of the planets in the zodiac circle are opposite. These directions of movement are called primary and secondary movements.
- If you measure segments of 30 degrees at the equator starting from the point of intersection with the horizon, you get 12 sectors.
- Draw a circle from the North through the top of the equatorial 30-degree sector. This line is called the arc of the astrological house or the house arc.
- If we draw arcs through all 12 vertices on the equator, we get 12 house arcs.
In the picture below, the arcs have a green light.
These house arcs will cross the zodiacal circle in 12 points. These are the cusps of houses in the Regiomontan system. As you can see, the astrological houses are unequal in length. In this example, the 11th and 12th houses are broad while the 1st is narrow.
If we measure 5 degrees on the equator in front of each 30-degree mark and then draw house arcs through these new marks, we will find spatial segments in front of each of the 12 houses. These segments symbolize areas where the planet belongs not to the current but to the next house. These areas in front of the houses are shaded in green.
Now we can project these spatial segments onto the zodiacal circle. As you can see, the wider the house, the wider the "gap" in front of it. So, for example, a planet 9 degrees from the top of the 12th house would already be considered inside the 12th house. And a planet near the narrow first house considers belonging the first house only if it is very close to its cusp.
Accounting for celestial latitude
The planets are not strictly on the zodiac circle but slightly above/below. This vertical deviation from the ecliptic plane is called the celestial latitude. See the example below. The Мoon is not strictly on the blue line but is slightly elevated above it. The red line represents the celestial latitude.
From the zodiac circle point of view, the Moon practically presses (almost coincides) with the top of the second house. But in the spatial sense, the Moon is outside the green-shaded sector. That is, it does not fall into the area of "capture" of the next house.
P.S. If you want to know the Moon's position with the highest possible accuracy, check out this article.
Another example. Venus is below the plane of the ecliptic. The red line shows its southern celestial latitude. Even visually, it is clear that Venus is in the zodiac circle, almost in the middle of the 12th house. But in the spatial sense, Venus fell into the green-shaded sector. So it already belongs to the 1st house.
It turns out that when considering the celestial latitude, we encounter unexpected deviations from the expected behavior. I do not think that Ptolemy, in his work, meant the use of celestial latitudes. The principle is simple: if he meant taking latitudes into account, he would mention it. In addition, the use of celestial latitude makes Ptolemy's 5-degree rule unpredictable and unobvious.
By default, the OLGA astroprocessor calculates the position in the houses, taking into account the five mundane degrees rule, considering the celestial latitude. No other program can do such a calculation.


